É, eu sei: estou indo de traz para a frente. Acho que na ilustração os blocos acabaram desenhados do mais elaborado para o mais simples. Então hoje é dia de falar de TRIÂNGULOS.
Os triângulos ferram com a vida da gente no patchwork. Ou ferrariam, se não fossemos espertas.... como eu já disse antes, patchwork é como lego - tudo tem de encaixar no tamanho certinho; enquanto estamos lidando com retângulos e quadrados, como na lição anterior, tudo bem. As peças são cortadas no fio do tecido. Mas quando lidamos com triângulos, somos obrigadas a cortar quadrados na diagonal para obtê-los; e aí pelo menos uma das extremidades da peça vai cair no viés do tecido.
E daí? Daí que o viés do tecido não tem estabilidade, deforma e estica facilmente, e o nosso cuidado em planejar a peça do tamanho certinho vai por água abaixo. Mas tem jeito de lidar com isso. Prova disso é esta peça, que fiz no ano passado; ela se chama "Pitágoras" e tem ziliões de triângulos - todos encaixados com perfeição:
Então está provado que tem jeito, sim. O segredo é: toda sub-unidade, todo bloco e toda peça tem de terminar com FIO do tecido em toda a volta. Por conta dessa regra, existem duas formas diferentes de cortar os triângulos, e hoje vamos falar do triângulinho que ocupa meio quadrado.
Olhe novamente o bloco estrela na ilustração do alto; repare que abaixo do desenho tem o mesmo bloco, mas todo subdividido em quadradadinhos; agora repare que todos os quadradinhos são formados por um par de triângulinhos. Ou seja, todos os triângulos ocupam meio quadrado.
Eu chamo essas subunidades de bipartidos. Se você sabe confeccioná-los, já pode fazer uma farra - brincar com eles e formar muitos blocos diferentes. Veja algumas possibilidades:
Para fazer um bipartido, você vai precisar cortar quadrados, e depois cortá-los na diagonal uma vez. O tamanho desse quadrado será o tamanho final de triângulo que você quer obter + 7/8". Sim, sete oitavos de polegadas.
MAS QUANTO MEDE ISSO?! Não importa. Você não precisa converter essa medida para centímetro. A régua de polegadas tem tudo lá marcadinho para você. Em uma lição futura vamos falar só da régua, certo?
Então vamos lá: o bloco estrela mede 8 polegadas segundo planejamos nossa peça de Natal lá nas primeiras lições. Se ele mede 8 polegadas, cada subunidade - ou cada bipartido - mede 2 polegadas. Se eu preciso de triângulos de 2 polegadas, vou cortar quadradinhos medindo 2 + 7/8; ao cortar esses quadradinhos na diagonal, obterei triângulos que medirão exatamente 2 polegadas + a margem de costura necessária.
Ficou assim nossa lista de corte (olhe na ilustração e acompanhe):
- preciso de 4 triângulos vermelhos - vou cortar 2 quadradinhos;
- preciso de 8 triângulos verdes - vou cortar 4 quadradinhos;
- preciso de 8 triângulos mostardas - vou cortar 4 quadradinhos;
- preciso de 12 triângulos brancos - vou cortar 6 quadradinhos.
Voilá!
E para costurar os quadradinhos, sejamos espertas novamente: juntar dois triângulos para costurar é um saco. O lance é o seguinte: costure primeiro e corte depois! Imagine que você quer um bipartido metade vermelho, metade branco. Faça assim:
Primeiro corte um quadradinho branco e um vermelho, no tamanho que você já sabe como calcular:
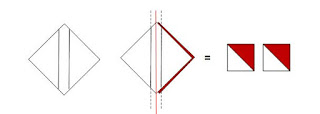
Faça dois riscos com lápis no avesso do quadradinho branco, partindo da diagonal - 1/4" para a esquerda e 1/4" para a direita; junte os dois quadrados, direito com direito, e costure em cima desses riscos; depois, corte no meio, como mostra a linha vermelha. Pronto, você tem duas unidades bipartidas e nem precisou pôr a mão em triângulos!
Agora faça o dever de casa: experimente, pratique e crie seus blocos. Divirta-se!
Até a próxima lição!





Adorei esse blog, porém acho mais difícil aprender em polegadas, sou iniciante, uma pena
ResponderExcluir